Modelling with a spreadsheet
Modelling with a spreadsheet
Use this spreadsheet to model what happens in an epidemic. You can input data into the cells with a yellow background (hover the mouse above these to see comments on the values that can be input). Change the initial conditions and see what happens to the progress of the disease.
- Does everyone who is susceptible catch the disease?
- Does everyone recover?
- How quickly does it last before dying out completely?
- What difference does it make if the disease can be fatal?
- Does the whole population ever die out?
- What difference does natural immunity and/or immunisation make?
- What figures on the spreadsheet give the reproductive ratio, R0?
- What value of R0 do we require for an epidemic not to occur?
- For a given value of R0 what level of vaccination do we need to prevent an epidemic occuring?
- What was R0 for SARS?
- What is R0 for measles?
- So what level of vaccination do we need for measles to prevent epidemics?
The mathematical model
Everything you need is on the Basic model worksheet in the spreadsheet. The Calculations worksheet is protected and cannot be changed to avoid the possibility of corrupting it. The spreadsheet gives a mathematical model of the progress of an infectious disease.
- What do we mean by a mathematical model?
- What is the difference between a mathematical model and reality?
- Why is a mathematical model useful?
- What are its limitations?
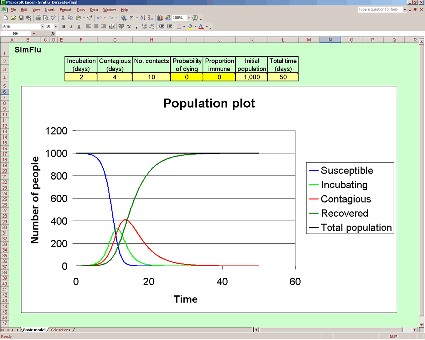
The cells with a yellow background are for you to input initial conditions. Light yellow cells cannot be zero, dark yellow ones can - and it is probably a good idea to give these a zero value to start with, then add in more complicating factors one by one. If you set the time period to 50 days to start with, you can then adjust this, according to the graph. For instance, the graph shown in the image above clearly shows little change after about 30 days, so the time period could be set to 30 days.
It is not possible to give a read out of the final figures for each of the subgroups shown in the graph, since the time period can be changed and this means that the final figure is not always in the same cell on the Calculations worksheet. You will need to estimate figures from the graph, therefore.
This model does not take all the possible factors into account. What other factors do you think should be taken into consideration if the model were further refined?


